Entrez un mot ou une phrase dans n'importe quelle langue 👆
Langue:
Traduction et analyse des mots par intelligence artificielle
Sur cette page, vous pouvez obtenir une analyse détaillée d'un mot ou d'une phrase, réalisée à l'aide de la meilleure technologie d'intelligence artificielle à ce jour:
- comment le mot est utilisé
- fréquence d'utilisation
- il est utilisé plus souvent dans le discours oral ou écrit
- options de traduction de mots
- exemples d'utilisation (plusieurs phrases avec traduction)
- étymologie
Qu'est-ce (qui) est Волны - définition
СТРАНИЦА ЗНАЧЕНИЙ В ПРОЕКТЕ ВИКИМЕДИА
Волны
изменения состояния среды (возмущения), распространяющиеся в этой среде и несущие с собой энергию. Например, удар по концу стального стержня вызывает на этом конце местное сжатие, которое распространяется затем вдоль стержня со скоростью около 5 км/сек; это - упругая В. Упругие В. существуют в твёрдых телах, жидкостях и газах. Звуковые В. (см. Звук) и Сейсмические волны в земной коре являются частными случаями упругих В. К электромагнитным волнам (См. Электромагнитные волны) относятся радиоволны, свет, рентгеновские лучи и др. Основное свойство всех В., независимо от их природы, состоит в том, что в виде В. осуществляется перенос энергии без переноса вещества (последний может иметь место лишь как побочное явление). Например, после прохождения по поверхности жидкости В., возникшей от брошенного в воду камня, частицы жидкости останутся приблизительно в том же положении, что и до прохождения В.
Волновые процессы встречаются почти во всех областях физических явлений; изучение В. важно и для физики и для техники.
В. могут различаться по тому, как возмущения ориентированы относительно направления их распространения. Так, например, звуковая В. распространяется в газе в том же направлении, в каком происходит смещение частиц газа (рис. 1, а), в В., распространяющейся вдоль струны, смещение точек струны происходит в направлении, перпендикулярном струне (рис. 1, б). В. первого типа называются продольными, а второго-поперечными.
В жидкостях и газах упругие силы возникают только при сжатии и не возникают при сдвиге, поэтому упругие деформации в жидкостях и газах могут распространяться только в виде продольных В. ("В. сжатия"). В твёрдых же телах, в которых упругие силы возникают также при сдвиге, упругие деформации могут распространяться не только в виде продольных В. ("В. сжатия"), но и в виде поперечных В. ("В. сдвига"). В твёрдых телах ограниченного размера (например, в стержнях, пластинках и т.п.) картина распространения В. более сложна, здесь возникают ещё и другие типы В., являющиеся комбинацией первых двух основных типов (подробнее см. Упругие волны).
В электромагнитных В. направления электрического и магнитного полей почти всегда (за исключением некоторых случаев распространения в несвободном пространстве) перпендикулярны направлению распространения В., поэтому электромагнитные В. в свободном пространстве поперечны.
Общие характеристики и свойства В. В. могут иметь различный вид. Одиночной В., или импульсом, называется сравнительно короткое возмущение, не имеющее регулярного характера (рис. 2, а). Ограниченный ряд повторяющихся возмущений называется цугом В. Обычно понятие цуга относят к отрезку синусоиды (рис. 2, б). Особую важность в теории В. имеет представление о гармонической В., т. е. бесконечной и синусоидальной В., в которой все изменения состояния среды происходят по закону синуса или косинуса (рис. 2, в); такие В. могли бы распространяться в однородной среде (если амплитуда их невелика) без искажения формы (о В. большой амплитуды см. ниже). Понятие бесконечной синусоидальной В., разумеется, является абстракцией, применимой к достаточно длинному цугу синусоидальных волн.
Основными характеристиками гармонической В. являются длина В. λ - расстояние между двумя максимумами или минимумами возмущения (например, между соседними гребнями или впадинами на поверхности воды) и период В. Т - время, за которое частица среды совершает одно полное колебание. Таким образом, бесконечная В. обладает строгой периодичностью в пространстве (что обнаруживается в случае, например, упругих В., хотя бы на моментальной фотографии В.) и периодичностью во времени (что обнаруживается, если следить за движением во времени определённой частицы среды). Между длиной В. λ и периодом Т имеется простое соотношение. Чтобы получить его, фиксируют внимание на частице, которая в данный момент времени находится на гребне В. После ухода от неё гребня она окажется во впадине, но через некоторое время, равное λ/с, где с - скорость распространения В., к ней подойдёт новый гребень, который в начальный момент времени был на расстоянии λ от неё, и частица окажется снова на гребне, как вначале. Этот процесс будет регулярно повторяться через промежутки времени, равные λ/с. Время λ /с совпадает с периодом колебания частицы Т, т. е. λ/с = Т. Это соотношение справедливо для гармонической В. любой природы.
Вместо периода Т часто пользуются частотой v, равной числу периодов в единицу времени: v = 1/Т. Между v и λ имеет место соотношение: λv = с. (В технике обычно вместо v применяют обозначение f.) В теории В. пользуются также понятием волнового вектора, по абсолютной величине равного k = 2π/λ = 2πv/c, т. е. равного числу В. на отрезке 2π и ориентированного в направлении распространения В.
Гармоническая В. Амплитуда и фаза. В гармонической В. изменения колеблющейся величины W во времени происходит по закону синуса (или косинуса) и описывается в каждой точке формулой: W = A sin 2πt/T (см. Колебания). Величина W в положении равновесия принята равной нулю. А - амплитуда В., т. е. значение, которое эта величина принимает при наибольших отклонениях от положения равновесия. В любой другой точке, расположенной на расстоянии r от первой в направлении распространения В., колебания происходят по такому же закону, но с запозданием на время t1 = r/c, что можно записать в виде:
W = A sin (2π/T) (t-t1) = A sin (2π/T) (t-r/c).
Выражение (φ = (2π/T) (t- r/c) называется фазой В. Разность фаз в двух точках r1 и r2 равна:
φ2 - φ1 = (2π/Tc) (r2 - r1) = (2π/λ) (r2 - r1).
В точках, отстоящих друг от друга на целое число В., разность фаз составляет целое число 2π, т. е. колебания в этих точках протекают синхронно - в фазе. Наоборот, в точках, отстоящих друг от друга на нечётное число полуволн, т. е. для которых r2 - r1 = (2N - 1)λ/2, где N = 1, 2..., разность фаз равна нечётному числу π, т. е. φ2 - φ1 = (2N - 1)π. Колебания в таких точках происходят в противофазе: в то время, как отклонение в одной равно А, в другой оно обратно по знаку, т. е. равно - А и наоборот.
Распространение В. всегда связано с переносом энергии, который можно количественно характеризовать вектором потока энергии 1. Этот вектор для упругих В. называется вектором Умова (по имени русского учёного А. А. Умова, введшего это понятие), для электромагнитных - вектором Пойнтинга. Направление вектора Умова совпадает с направлением переноса энергии, а абсолютная величина равна энергии, переносимой В. за единицу времени через площадку 1 см2, расположенную перпендикулярно вектору I. При малых отклонениях от положения равновесия I = КА, где К - коэффициент пропорциональности, зависящий от природы В. и свойств среды, в которой В. распространяется.
Поверхности равных фаз, фронт В. Важной характеристикой В. является вид поверхностей равных фаз, т. е. таких поверхностей, в любой точке которых в данный момент времени фазы одинаковы. Форма поверхности равной фазы зависит от условий возникновения и распространения В. В простейшем случае такими поверхностями являются плоскости, перпендикулярные направлению распространения В., а В. называется плоской. В., у которых поверхностями равных фаз являются сферы и цилиндры, называются соответственно сферическими и цилиндрическими. Поверхности равных фаз называются также фронтами В. В случае конечной или одиночной В. фронтом называется передний край В., непосредственно граничащий с невозмущённой средой.
Интерференция В. При приходе в данную точку среды двух В. их действие складывается. Особо важное значение имеет наложение так называемых когерентных В. (т. е. В., разность фаз которых постоянна, не меняется со временем). В случае когерентности В. имеет место явление, называемое интерференцией: в точках, куда обе В. приходят в фазе, они усиливают друг друга; в точках же, куда они попадают в противофазе, - ослабляют друг друга. В результате получается характерная интерференционная картина (см., например, рис. 3). См. также Интерференция света, Когерентность.
Стоячие В., собственные колебания. При падении плоской В. на плоское же отражающее препятствие возникает отражённая плоская В. Если при распространении В. в среде и при отражении их от препятствия не происходит потерь энергии, то амплитуды падающей и отражённой В. равны между собой. Отражённая В. интерферирует с падающей В., в результате чего в тех точках, куда падающая и отражённая В. приходят в противофазе, результирующая амплитуда падает до 0, т. е. точки всё время остаются в покое, образуя неподвижные узлы колебаний, а в тех местах, где фазы В. совпадают, В. усиливают друг друга, образуя пучности колебаний. В результате получается так называемая стоячая В. (рис. 4). В стоячей В. поток энергии отсутствует: энергия в ней (при условии, что потерь нет) перемещается только в пределах, ограниченных смежными узлом и пучностью.
Стоячая В. может существовать также и в ограниченном объёме. В частности, в случае, изображённом на рис. 4, на месте ВВ можно вообразить себе такое же препятствие, что и справа. Между двумя стенками будет существовать стоячая В., если расстояние между ними равно целому числу полуволн. Вообще стоячая В. может существовать в ограниченном объёме лишь в том случае, если длина В. находится в определённом соотношении с размерами объёма. Это условие выполняется для ряда частот v1, v2, v3,..., называется собственными частотами данного объёма.
Дифракция. При падении В. на непрозрачное для неё тело или на экран позади тела образуется теневое пространство (заштриховано на рис. 5, а и 5, б). Однако границы тени не резки, а размыты, причём размытость увеличивается при удалении от тела. Это явление огибания тела В. называется дифракцией. На расстояниях порядка d2/λ от тела, где d - его поперечный размер, тень практически полностью смазана. Чем больше размеры тела, тем большее пространство занимает тень. Тела, размеры которых малы по сравнению с длиной В., вообще не создают тени, они рассеивают падающую на них В. во всех направлениях. Изменение амплитуды В. при переходе из "освещённой" области в область тени происходит по сложному закону с чередующимися уменьшением и увеличением амплитуды (рис. 6, а и 7), что обусловлено интерференцией В., огибающих тело.
Дифракция имеет место также при прохождении В. через отверстие (рис. 5, б и 6, б), где она также выражается в проникновении В. в область тени и в некотором изменении характера В. в "освещённой" области: чем меньше диаметр отверстия по сравнению с длиной В., тем шире область, в которую проникает В. См. также Дифракция света.
Поляризация В. Как уже сказано, плоскость, в которой происходят колебания поперечной В., перпендикулярна направлению распространения. Эта особенность поперечных В. обусловливает возможность возникновения явления поляризации, которая заключается в нарушении симметрии распределения возмущений (например, смещений и скоростей в механических В. или напряжённостей электрических и магнитных полей в электромагнитных В.) относительно направления распространения. В продольной В., в которой возмущения всегда направлены вдоль направления распространения В., явления поляризации возникнуть не могут.
Если колебания возмущения Е происходят всё время в каком-то одном направлении (рис. 8, а), то имеет место простейший случай линейно-поляризованной, или плоско-поляризованной В. Возможны и другие, более сложные типы поляризации. Например, если конец вектора Е, изображающего возмущение, описывает эллипс или окружность в плоскости колебаний (рис. 8, б), то имеет место эллиптическая или круговая поляризация. Скорость распространения поперечных В. может зависеть от состояния поляризации.
Поляризация может возникнуть: из-за отсутствия симметрии в возбуждающем В. излучателе, при распространении В. в анизотропной среде (см. Анизотропия), при преломлении и отражении В. на границе двух сред. Подробнее см. Поляризация света.
Отражение и преломление В. При падении на плоскую границу раздела двух разных сред плоская В. частично отражается, частично проходит в другую среду, оставаясь плоской, но меняет при этом своё направление распространения (преломляется) (рис. 9, а). Углы, образуемые направлениями падающей, отражённой и преломлённой В. (рис. 9, б) с перпендикуляром к границе раздела сред, называются соответственно углом падения α, углом отражения α1 и углом преломления α2. Согласно закону отражения, угол падения равен углу отражения, т. е. α = α1. Согласно закону преломления, синус угла падения относится к синусу угла преломления, как скорость в первой среде к её скорости во второй среде, т. е.:
sin α/sin α2 = с1/с2 = n,
где n - показатель преломления (см. также Отражение света, Преломление света).
Смесь В. с различными состояниями поляризации, распространяющаяся в одном и том же направлении, разделится, попадая в среду, в которой скорость распространения зависит от состояния поляризации; В., поляризованные различно, пойдут по разным направлениям (Двойное лучепреломление). Во многих случаях скорость распространения зависит также от частоты колебаний (Дисперсия, см. ниже); в этих случаях смесь В. с различными частотами при преломлении разделится. При отражении расходящейся (сферической или цилиндрической) В. под малыми углами к плоской границе раздела двух сред возникают некоторые особенности. Наиболее важна та, когда скорость c2 в нижней среде больше, чем c1 в верхней среде (рис. 10), тогда, кроме обычной отражённой В., которой соответствует луч ОАР, возникает так называемая боковая В. Соответствующий ей луч OSDP часть своего пути (отрезок SD) проходит в среде, от которой происходит отражение.
Форма В. Дисперсия и нелинейность В. В процессе распространения В. её форма претерпевает изменения. Характер изменений существенно зависит от первоначальной формы В. Лишь бесконечная синусоидальная (гармоническая) В. (за исключением В. очень большой интенсивности) сохраняет свою форму неизменной при распространении, если при этом она не испытывает заметного поглощения. Но всякую В. (любой формы) можно представить как сумму бесконечных синусоидальных В. разных частот (как говорят, разложить в спектр). Например, одиночный импульс можно представить, как бесконечную сумму наложенных друг на друга синусоидальных В. Если среда, в которой распространяются В., линейна, т. е. её свойства не меняются под действием возмущений, создаваемых В., то все эффекты, вызываемые негармонической В., могут быть определены как сумма эффектов, создаваемых в отдельности каждой из её гармонических составляющих (так называемый Суперпозиции принцип).
В реальных средах нередко скорости распространения синусоидальных В. зависят от частоты В. (так называемая дисперсия волн). Поэтому негармоническая В. (т. е. совокупность гармонических В. различных частот) в процессе распространения меняет свою форму вследствие того, что при распространении этих гармонических В. соотношение между их фазами меняется. Искажение формы В. может происходить и при дифракции и рассеянии негармонических В., так как оба эти процесса зависят от длины В. и поэтому для гармонической В. разной длины дифракция и рассеяние будут происходить по-разному. При наличии дисперсии изменение формы негармонической В. может происходить также в результате преломления В. Однако иногда может искажаться и форма гармонической В. Это происходит в тех случаях, когда амплитуда распространяющейся В. достаточно велика, так что уже нельзя пренебрегать изменениями свойств среды под воздействием В., т. е. когда сказываются нелинейные свойства среды. Искажения формы синусоидальной В. могут выразиться в том, что "горбы" В. (области больших возмущений) распространяются со скоростью, превышающей скорость распространения остальных участков В., в результате чего синусоидальная форма В. превращается в пилообразную (рис. 11). В нелинейной среде существенно изменяются и другие законы распространения В. - в частности, законы отражения и преломления. Подробнее см. Нелинейная оптика.
Фазовая и групповая скорости В. Введённая выше скорость В. называется фазовой скоростью, это скорость, с которой перемещается какая-нибудь определённая фаза бесконечной синусоидальной В. (например, фаза, соответствующая гребню или впадине), фазовая скорость В. входит, в частности, в формулу закона преломления. Однако на опыте имеют дело с В. не в виде бесконечных синусоид, называемых также монохроматическими В., для которых только и имеет смысл понятие фазовой скорости, а с ограниченными В. Как уже было указано, любая ограниченная В. может быть представлена в виде наложения большого (точнее - бесконечно большого) числа монохроматических В. различных частот. Если фазовые скорости В. всех частот одинаковы, то с этой же скоростью распространяется и вся совокупность, или группа, В. Если же эти скорости не одинаковы, т. е. имеет место дисперсия, то вопрос о скорости распространения ограниченной. В. усложняется. Английским физиком Дж. У. Рэлеем было показано, что если ограниченная В. составляется из В., частоты которых мало отличаются друг от друга, то эта В., или как её часто называют волновой пакет, распространяется с определённой скоростью, называемой групповой скоростью. Групповая скорость u вычисляется по формуле: u = с - λdc/dλ. С групповой скоростью происходит также перенос энергии В.
Изменение частоты В. при движении источника или наблюдателя (эффект Доплера). Наблюдатель, движущийся по направлению к источнику В. (любого вида), воспринимает несколько повышенную частоту по сравнению с неподвижным наблюдателем, между тем как наблюдатель, удаляющийся от источника В., воспринимает пониженную частоту. Аналогичное явление (качественно) имеет место также, когда наблюдатель неподвижен, а источник В. движется. Это явление называется Доплера эффектом.
В. и лучи. Линия, направление которой в каждой точке совпадает с направлением потока энергии в В., называется лучом (рис. 9, б). В изотропной среде это направление совпадает с направлением нормали к фронту В. Плоской В. соответствует параллельный пучок прямолинейных лучей, сферической В. - радиально расходящийся пучок и т.д. При некоторых условиях сложный расчёт распространения В. можно заменить более простым расчётом формы лучей. Этим пользуются в геометрической акустике (См. Геометрическая акустика) и геометрической оптике (См. Геометрическая оптика). Такой упрощённый подход применим, когда длина В. достаточно мала по сравнению с некоторыми характерными размерами, например размерами препятствий, лежащих на пути распространения В., поперечными размерами фронта В., расстояний до точки, в которой сходятся В., и т.п.
Излучение и распространение В. Для излучения В. необходимо произвести в среде некоторое возмущение за счёт внешнего источника энергии. Работа, совершаемая этим источником, за вычетом некоторых потерь превращается в энергию излучаемых В. Так, например, мембрана телефона или диафрагма громкоговорителя, получая энергию от электроакустического преобразователя (См. Электроакустические преобразователи), излучает звуковые В. Излучение В. производится всегда источниками ограниченных размеров, в результате чего возникает "расходящаяся" В. Только на достаточно большом расстоянии от источника эту В. можно принять за плоскую.
Несмотря на разную природу В., закономерности, которыми определяется их распространение, имеют между собой много общего. Так, упругие В. в однородных жидкостях (газах) или электромагнитные В. в свободном пространстве (а в некоторых случаях и в пространстве, заполненном однородным изотропным диэлектриком), возникающие в какой-нибудь малой области ("точке") и распространяющиеся без поглощения в окружающем пространстве, подчиняются одному и тому же волновому уравнению (См. Волновое уравнение).
Особого вида излучение В. имеет место при движении в среде тел со скоростями, большими, чем фазовые скорости В. в этой среде. Электрон, движущийся в какой-либо среде со скоростью, большей, чем фазовая скорость электромагнитных В., в этой среде излучает В. (Черенкова - Вавилова излучение (См. Черенкова-Вавилова излучение)), при движении же со скоростью, меньшей фазовой скорости света в среде, это движение сопровождается лишь простым перемещением электрического и магнитного полей без перехода энергии движения в энергию излучения. Аналогично этому самолёт, движущийся со скоростью, большей скорости звука, излучает звуковую В. особого вида - ударную волну (См. Ударная волна), и теряет на это определённую часть энергии. Излучением В. такого же происхождения, распространяющихся по поверхности воды, объясняется появление волнового сопротивления (См. Волновое сопротивление) при движении корабля.
Другие виды В. Известны также: а) температурные В., распространяющиеся в окрестности переменного во времени источника тепла; б) вязкие В. - поперечные (быстро затухающие) В. в вязкой жидкости; в) Волны де Бройля, которыми в квантовой механике описывается поведение микрочастиц; г) Гравитационные волны, излучаемые движущимися с ускорением массами.
Лит.: Горелик Г. С., Колебания и волны, 2 изд., М., 1959; Красильников В. А., Звуковые и ультразвуковые волны в воздухе, воде и твердых телах, 3 изд., М., 1960; Бреховских Л. М., Волны в слоистых средах М., 1957.
Л. М. Бреховских.
Рис. 1. а - продольная волна; б - поперечная волна.
Рис. 2. а - одиночная волна; б - цуг волн; в - бесконечная синусоидальная волна.
Рис. 4. Стоячая волна, возникшая в результате интерференции падающей и отраженной от препятствия АА волны; в точке а - узел колебания, в точках b - пучности.
Рис. 5. Образование тени при падении волны: а - на непрозрачное тело; б - на отверстие в непрозрачном экране (d - paзмер тела или отверстия).
Рис. 8. а - линейно-поляризованная волна; б - волна, поляризованная по кругу (Е - вектор, изображающий распространяющееся возмущение).
Рис. 9. а - схема отражения и преломления плоской волны λ1 - длина падающей и отраженной волны, λ2 - длина преломленной волны); б - стрелки, изображающие лучи, соответствующие падающей отраженной и преломленной волнам.
Рис. 10. Схема образования боковой волны.
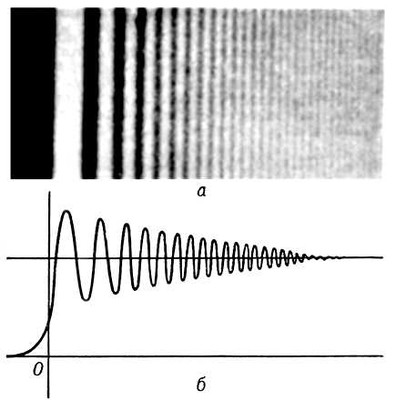
Рис. 7. а - дифракция света от края экрана; виден сложный переход от света к тени; б - кривая, характеризующая освещенность пространства между светом и тенью; край экрана в точке О.
Рис. 3. Интерференция волн на поверхности воды, возбуждаемых в двух различных точках.
Рис. 11. Искажение формы синусоидальной волны большой интенсивности. На некотором расстоянии синусоидальная волна а превращается в пилообразную г (б и в - промежуточные стадии). Направление распространения волны справа налево.
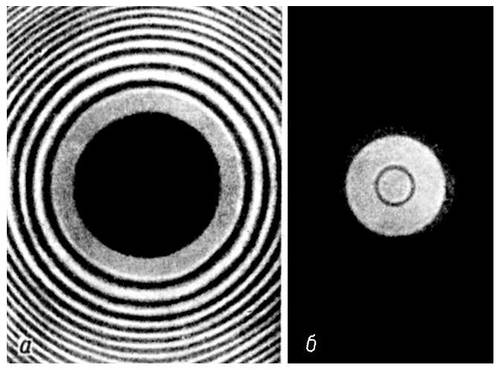
Рис. 6. Дифракционная картина при падении света: а - на круглый экран; б - на круглое отверстие.
ВОЛНЫ
возмущения, распространяющиеся с конечной скоростью в пространстве и несущие с собой энергию без переноса вещества. Наиболее часто встречаются упругие волны, напр., звуковые, волны на поверхности жидкости и электромагнитные волны. Несмотря на разную природу, все волны подчиняются общим закономерностям. Если возмущение ориентировано вдоль направления распространения, волна называется продольной (напр., звуковая волна в газе); если же возмущение лежит в плоскости, перпендикулярной направлению распространения, волна называется поперечной (напр., упругая волна, распространяющаяся вдоль струны, электромагнитная волна в свободном пространстве). В простейшем случае плоской гармонической волны изменения колеблющейся величины y в точке, отстоящей на расстоянии x от источника возмущений, во времени t происходят по закону: где А - амплитуда колебания, ? - длина волны, Т - период колебаний. Более сложные волны можно представить в виде суперпозиции гармонических волн.
волны
мн.
1) Колебательные движения в физической среде, способные распространяться от места возникновения.
2) разг. Радиоволны.
1) Колебательные движения в физической среде, способные распространяться от места возникновения.
2) разг. Радиоволны.
Wikipédia
Волны
Волны:
- Волны (в физике) — изменение состояния среды (возмущение), распространяющееся в этой среде и переносящее с собой энергию.
- «Волны» — роман Вирджинии Вулф.
- «Волны» — фильм 2019 года производства США.
- «Волны» — альбом группы «А’Студио».
- «Волны» — совместный альбом лидера рок-группы «АукцЫон» Леонида Фёдорова и контрабасиста Владимира Волкова.
Exemples du corpus de texte pour Волны
1. - Высота волны цунами сравнима с высотой волны океанского прилива.
2. Волны пропагандистского тоталитаризма захлестывают.
3. Это пример волны, которая хлынула в язык, из этой волны осталось несколько словечек.
4. На ночном течении Волны появляются, Волны проявляются К месяцу с почтением.
5. Характер новой волны Можем ли мы сегодня определить характер следующей длинной волны?
